Appearance
1 进制与进制转换
1.1 进制
1 进制的概念
进制也就是进位制,是人们规定的一种进位方法。 对于任何一种进制---X进制,就表示某一位置上的数运算时是逢X进一位。
十进制是逢十进一,十六进制是逢十六进一,二进制就是逢二进一。
十进制使用10个数字表示:0、1、2、3、4、5、6、7、8、9
二进制使用两个数字表示:0、1
八进制使用八个数字表示:0、1、2、3、4、5、6、7
十六进制使用十六个数字表示:0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F(不区分大小写),A相当于十进制的10,F相当于十进制的15。
2 二进制与十六进制
人类为什么使用十进制?
我觉得应该是人类有10个手指头,如果有8个手指头肯定使用的是八进制,有16个手指头肯定使用的就是十六进制了。
关于十进制,大家太了解了,不过多解释了。
那么计算机为什么使用的是二进制呢?
因为计算机是靠集成电路运行的,有电经过电子元器件就表示1,没电经过电子元器件就表示0,用两种状态表示,信号的抗干扰性也更强。
为什么计算机中还会用到十六进制呢?
二进制对于计算机来说是一种很方便的计数方法,但是二进制对于人类来说很难使用,因为数字太长了,例如 0000 1010 1111 0101 1000 1111 11111 1111。
而1位十六进制数字可以代表4位二进制数字,例如 FF 刚好等于 1111 1111,二进制和十六进制之间的转换很方便(进制转换后面再讲),所以说用十六进制表达二进制字符串无疑是最佳的方式。
十进制是逢十进一,二进制是逢二进一,十六进制就是逢十六进一,所以用二进制从 0 到 31 的计数如下:
| 十进制 | 二进制 | 十六进制 | 十进制 | 二进制 | 十六进制 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 16 | 10000 | 10 |
| 1 | 1 | 1 | 17 | 10001 | 11 |
| 2 | 10 | 2 | 18 | 10010 | 12 |
| 3 | 11 | 3 | 19 | 10011 | 13 |
| 4 | 100 | 4 | 20 | 10100 | 14 |
| 5 | 101 | 5 | 21 | 10101 | 15 |
| 6 | 110 | 6 | 22 | 10110 | 16 |
| 7 | 111 | 7 | 23 | 10111 | 17 |
| 8 | 1000 | 8 | 24 | 11000 | 18 |
| 9 | 1001 | 9 | 25 | 11001 | 19 |
| 10 | 1010 | A | 26 | 11010 | 1A |
| 11 | 1011 | B | 27 | 11011 | 1B |
| 12 | 1100 | C | 28 | 11100 | 1C |
| 13 | 1101 | D | 29 | 11101 | 1D |
| 14 | 1110 | E | 30 | 11110 | 1E |
| 15 | 1111 | F | 31 | 11111 | 1F |
八进制用的不多,原理是一样的,就不解释了。
1.2 进制转换
什么是进制转换?
就是十进制和二进制的相互转换,十进制和十六进制的相互转换、二进制和十六进制的相互转换等。
进制转换就是用不同的计数法来表示同一个数字。
例如看到二进制 11010,你很难知道它是多少,换算成十进制为 26,你才知道它是多少。
1 十进制转二进制
十进制转换为二进制用的是除二取余的方法。
举个栗子,将十进制的26转换为二进制:
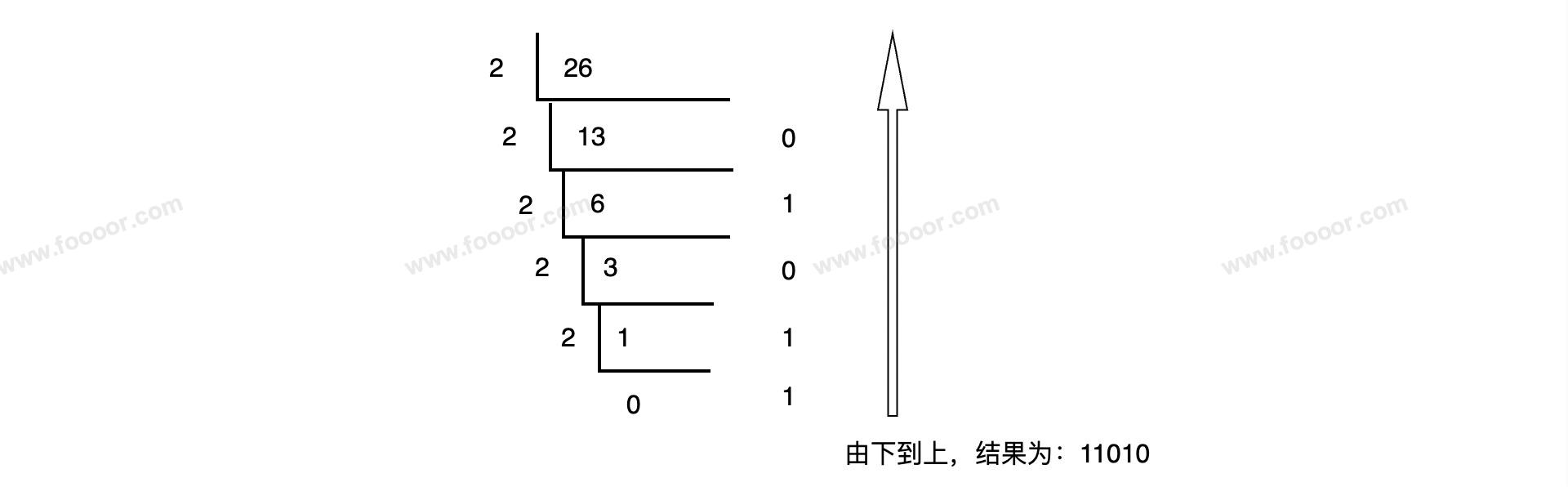
求取过程说明:
将26除以2,商为13,余数为0,将商继续除以2,商为6,余数位1,继续将商除以2……,直到商为0,然后将所有的余数按从后到前的顺序排列起来,就得到了二进制的结果。
2 十进制转十六进制
和十进制转换为二进制是类似的,不过是除16取余。
举个栗子,将十进制的6700转换为十六进制:
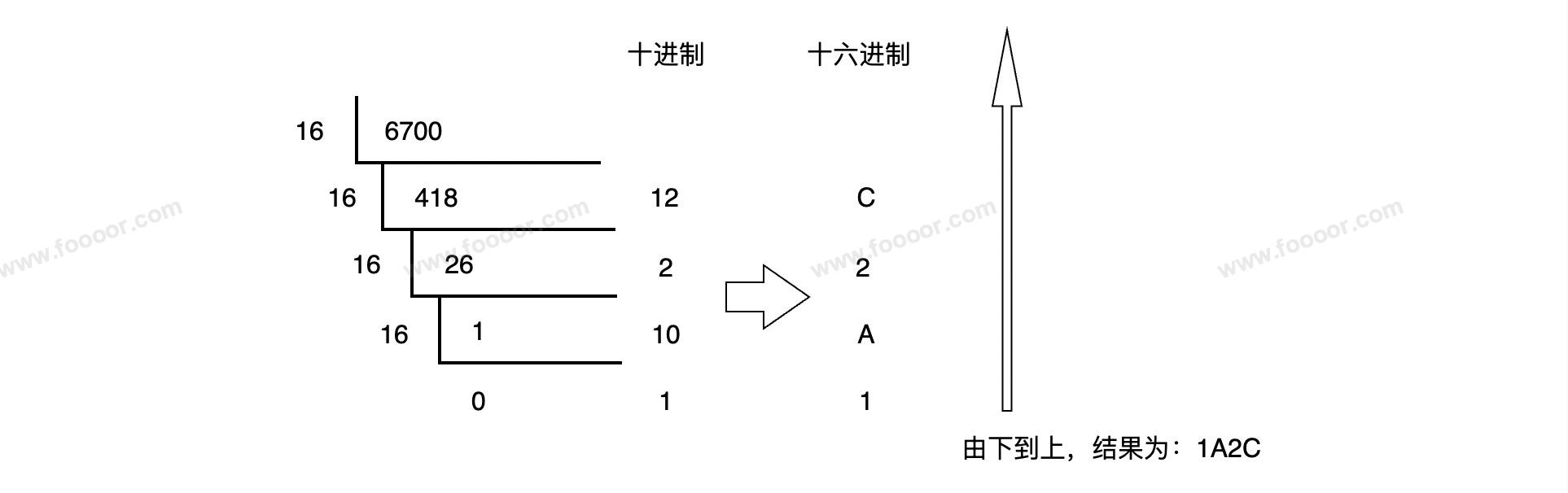
求取过程说明:
将6700除以16,商为418,余数为12,继续将商418除以16,商为26,余数为2,继续将商除以16……,直到商为0,然后将得到的余数按照从后到前的顺序排列起来,注意,余数要转换为十六进制进行排列,得到的结果就是十六进制的结果了。
3 二进制和十六进制转十进制
将 2 、3 、6 和 5 转换为十进制的 2365, 可以使用如下方式计算:
(2 * 10^3) + (3 * 10^2) + (6 * 10^1) + (5 * 10^0) = 2000 + 300 + 60 + 5 = 2365
以同样的方式,我们可以将二进制和十六进制转换为十进制。
举个栗子:
将二进制的 11010 转换为十进制:
(1 * 2^4) + (1 * 2^3) + (0 * 2^2) + (1 * 2^1) + (0 * 2^0) = 16 + 8 + 0 + 2 + 0 = 26
将十六进制的 1A2C 转换为十进制,注意要将字母转成10进制进行计算:
(1 * 16^3) + (10 * 16^2) + (2 * 16^1) + (12 * 16^0) = 4096 + 2560 + 32 + 12 = 6700
其他进制转十进制通过类似的方式转换即可。
4 二进制与十六进制互转
相对于十进制和二进制、十进制和十六进制的转换,二进制和十六进制之间的转换就显得简单很多。
将二进制转十六进制,首先将二进制数字从右边开始,每4位分成一组,如果最左边一组的二进制不足4位,则在左边补零。然后将每一组二进制转换为对应的十六进制数字即可。
举个栗子:将二进制 11010 转换为十六进制:
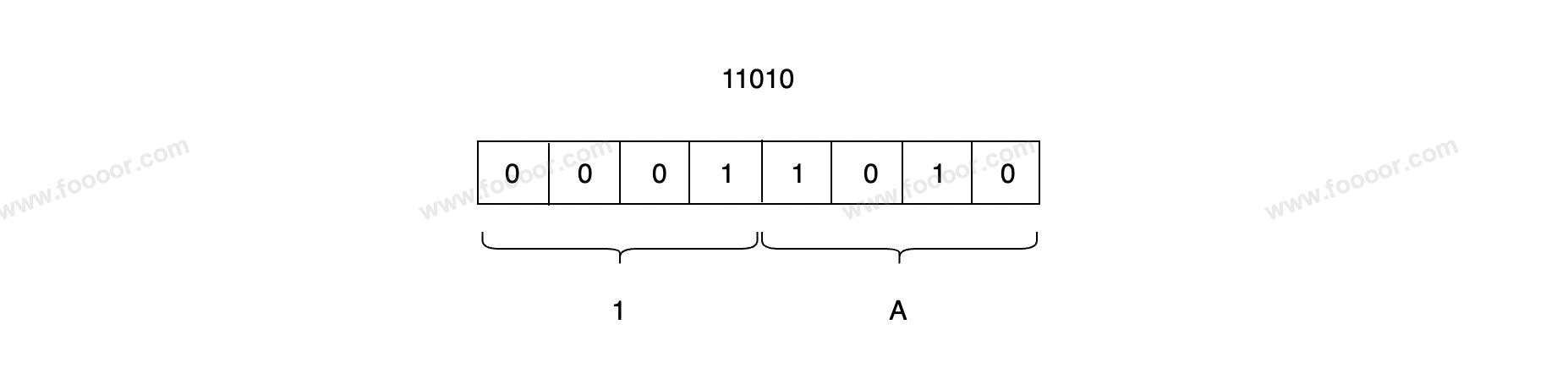
所以将二进制的 11010 转换为十六进制为 1A。
同样,十六进制转二进制也是将每一个十六进制数字替换为4个二进制数字即可。
举个栗子:将十六进制 1A2C 转换为二进制:
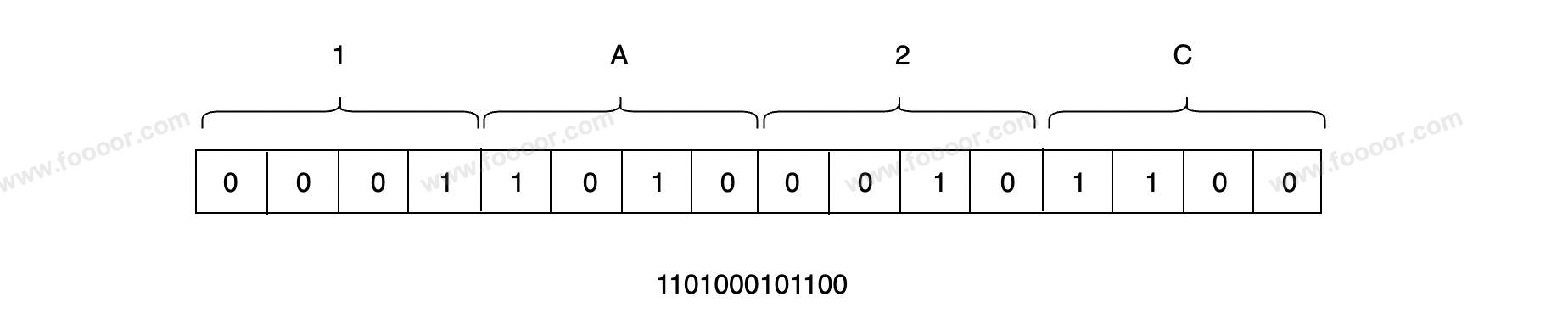
所以十六进制的 1A2C 等于 二进制的 1101000101100 。
1.3 各进制数字的表示方法
在写代码的时候,我如果写了一个 110,你知道它是多少进制的吗?
为了区分各个进制的数字,在大多数的编程语言中,使用如下方式区分各个进制的数字。
二进制(Binary)
以 0 和 1 表示;在编程中,使用前缀
0b或0B表示二进制数。例如:
0b1010表示十进制的 10。八进制(Octal)
以 0-7 表示;在编程中,使用前缀
0表示八进制数。例如:
0377表示十进制的 255。十进制(Decimal)
以 0-9 表示;在编程中,十进制是最常用的表示方式,一般写的数字默认就是十进制。
例如:
123。十六进制(Hexadecimal)
以 0-9 和 A-F(或 a-f)表示,A 表示 10,B 表示 11,...,F 表示 15;在编程中,使用前缀
0x或0X表示十六进制数。例如:
0xFF表示十进制的 255。