# 3 原码反码补码
原码、反码、补码是计算机中数值的三种表示方法，至于为什么会有原码、反码、补码，继续看了你就明白。
# 3.1 原码
# 1 什么是原码
原码就是数值最直观的表示方法。就是将数值直接转换为二进制。
第一位表示符号位，0为正数，1为负数。
举个栗子：以下以一个字节的数值进行演示，为了便于阅读，中间加个空格。
5 的原码是：
0000 0101
-5 的原码就是：
1000 0101
看上去没什么问题，但是其实有很大的局限性。
# 2 原码的问题
有两个 0
你会发现原码表示数值的方法，会出现两个 0，
0000 0000 表示的是 +0，1000 0000 表示的是 -0 ，这不科学啊，0 就是 0，没有符号一说。
不好运算
用原码来计算 1 + 1 = 2
0000 0001 + 0000 0001 = 0000 0010
0000 0010 是 2，没问题。
再计算 1 + (-1) = 0
0000 0001 + 1000 0001 = 1000 0010
1000 0010 是 -2 ，1 + (-1) = -2 ？，不能这么搞。
所以可以看到，使用原码来表示数值，0 有两种表现形式，这个很不方便。另外进行运算的时候，正数相加是没有问题的，但是正负相加和负负相加都会出问题，而且在进行正负运算的时候，还要考虑符号位，为了解决原码的问题，引出反码。
# 3.2 反码
# 1 什么是反码
反码表示方式在原码的基础上对负数进行取反操作。
所以：正数的反码还是等于原码；负数的反码就是它的原码除符号位外，按位取反。
举个栗子：
5 的原码和反码
原[0000 0101]
反[0000 0101]
2
-5 的原码和反码
原[1000 0101]
反[1111 1010]
2
# 2 反码的问题
用反码来计算 1 + (-1) = 0
0000 0001 + 1111 1110 = 1111 1111
1111 1111 是 -0 的反码 ，正确了！
再计算 (-1) + (-3) = -4
1111 1110 + 1111 1100 = 1111 1010
1111 1010 是 -5 的反码，又不对了。
所以反码还是有问题，0还是有两种表示方法，负数相加也有问题。
因此继续引出补码。
# 3.3 补码
# 1 什么是补码
解决了原码和反码的问题，引入了补码。
在补码中，正数的补码还是等于原码，而负数的补码是其反码加1。
举个栗子：
5 的原码、反码、补码
原[0000 0101]
反[0000 0101]
补[0000 0101]
2
3
-5 的原码、反码、补码
原[1000 0101]
反[1111 1010]
补[1111 1011]
2
3
# 2 补码的运算
用补码来计算 1 + (-1) = 0
0000 0001 + 1111 1111 = 0000 0000
溢出的部分被忽略，所以结果是 0，正确。
再计算 (-1) + (-3) = -4
1111 1111 + 1111 1101 = 1111 1100
1111 1100 是 -4 的补码，正确。
终于完美了。
可以看到补码的运算不用考虑符号位，而且只有1个0，就是 0000 0000。
第一位是符号位，那么 1000 0000 这个原码是 -0 的数字补码表示多少呢？
看下面的列表：
| 数值 | 补码 | 数值 | 补码 |
|---|---|---|---|
| 0 | 0000 0000 | -1 | 1111 1111 |
| 1 | 0000 0001 | -2 | 1111 1110 |
| 2 | 0000 0010 | -3 | 1111 1101 |
| 3 | 0000 0011 | -126 | 1000 0010 |
| -127 | 1000 0001 | ||
| -128 | 1000 0000 |
如果只考虑一个字节存储数值的时候，用补码表示，1000 0000 表示的 -128 ，这是通过推算出来的， -127 - 1 = -128，所以 -128 并没有原码和反码表示。
用 1000 0000 表示 -128 ，既解决了两个 0 的问题，也解决了运算问题，运算时也不用考虑符号位，还能多存储一个 -128。
所以使用一个字节存储数据的时候，表示范围在 [-128 ~ 127]，就是这么来的。
# 3.4 总结
所以在计算机中，所有的数据都是以补码的形式存储的。因为正数的原码是自己，所以看上去以为是原码。
例如给了一个二进制数字 1110 0011 ，这个数字是多少呢？
则通过补码计算原码，举个栗子：
1110 0011 # 符号位是1，表示负数
1110 0010 # -1，得到反码
1001 1101 # 除符号位外取反，得到原码
然后再二进制转十进制：2^0 + 2^2 + 2^3 + 2^4 = 29
2
3
4
所以 计算机中二进制数都是补码的表示方法！二进制数都是补码的表示方法！！二进制数都是补码的表示方法！！！
而且计算机只会加法，减法也是加上一个负数，运算的时候也不用对考虑符号位特殊处理，符号位也直接参与运算。
原码和反码只是让人类能理解这个逻辑，在计算机中是不需要的。
# 3.5 补码的思想
我们前面说了，正数的补码和原码相同，而负数的补码是其反码加1。
但这只是计算补码的方式，不是补码原来的定义。
一个钟表，调时间的时候，可以正转去调，也可以反转去调。
现在是10点，要调到8点，可以逆时针倒拨2小时，也可以正拨10小时，效果是一样的。
所以对于钟表而言， 10 - 2 = 8，10 + 10 = 8 ，没毛病吧。
所以在钟表里，12称之为模，超过了12就会重新从1开始算了。
通过这种方式，不用再做减法了，减去一个数，就等于加上另一个数，所有运算都用加法就好了。
补码也是类似的原理。
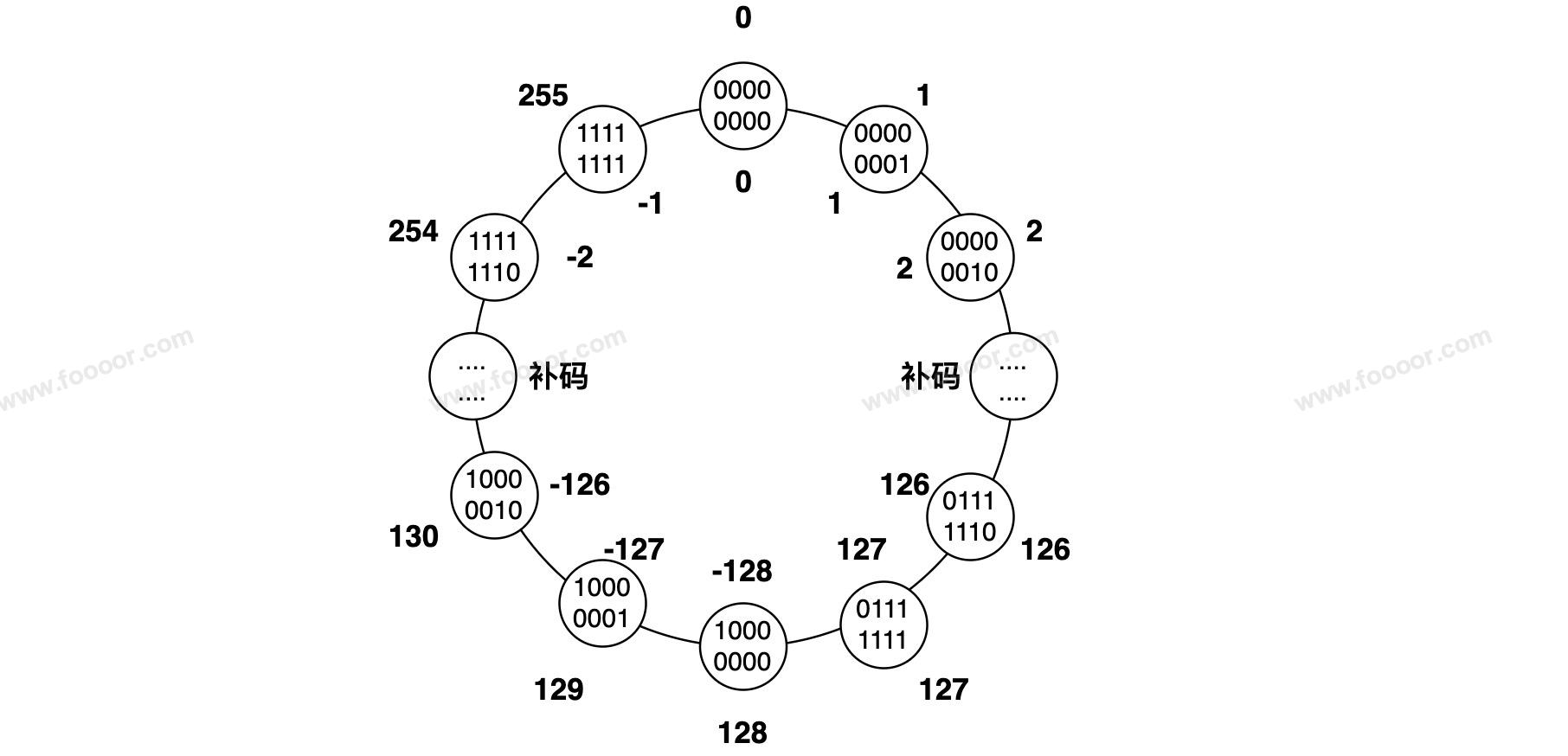
上面的图，从0000 0000 ~ 1111 1111，总共是256个数字，可以看出：
1 - 2 = -1 ，同样 1 + 254 = -1，也就是 0000 0001 + 1111 1110 = 1111 1111
而 254 的 1111 1110 就是 -2 的补码。
← 02-位与字节